Hola..kohvic kini kembali lagi untuk membuat
tulisan berikutnya. Biasa lar, selama ini saia menghilang karena mengumpulkan
bahan tulisan di sela-sela kesibukan bekerja..heheheh. Oke, pada kesempatan
kali ini saia akan membahas tentang Hidden Markov Model. Well, sebenarnya topik
ini sudah pernah dibahas bersama dengan pemodelan statistik urutan PSSM pada
tulisan sebelumnya. Namun disini saia ingin membahas secara khusus dan mendalam
mengenai hidden Markov model ini. Seperti yang kita tahu bahwa Hidden Markov
model banyak digunakan dalam berbagai pemodelan probabilitas urutan DNA atau
protein. Aplikasi dari pemodelan ini cukup beragam, mulai dari penjajaran
urutan banyak, prediksi gen, hingga prediksi famili dan struktur protein. Namun sebelum
beranjak langsung ke permasalahan real, saia ingin mengenalkan konsep HMM
menggunakan contoh sederhana terlebih dahulu, pelemparan koin.
Bayangkan bahwa kita sedang bertaruh pada
permainan melempar koin. Seperti yang kita tahu, hasil dari pelemparan koin ada
dua, yakni bagian muka (saia singkat M) dan belakang (saia singkat B). Nah, ditambah
dengan sedikit bumbu dramatisasi, si bandar atau pelempar koin ternyata sedikit
bermain curang. Selain menggunakan koin yang standar (S), ternyata si bandar
menggunakan koin non-standar (N) yang memiliki tampilan sama, namun memberikan
distribusi peluang hasil yang berbeda dengan koin standar. Katakanlah, peluang
munculnya bagian muka (M) dan belakang (B) masing-masing adalah 0,5 pada koin
standar (S); sedangkan pada koin non-standar (N) peluang munculnya M dan B
masing-masing adalah 0,75 dan 0,25. Dalam melakukan aksinya, si bandar sesekali
menukar koin secara diam-diam. Nah pesan moral yang didapatkan dari certa di
atas adalah jangan berjudi yah karena judi itu tidak baik. Errr….maaf kembali
ke topik. Oke, sekarang apa hubungannya cerita di atas dengan hidden Markov
model? Well, pada cerita di atas tentu saja si bandar tidak akan begitu baiknya
memberi tahu mana koin S dan mana koin N. Satu-satunya informasi yang kita tahu
adalah urutan kemunculan bagian muka M dan belakang B dari setiap pelemparan
koin.
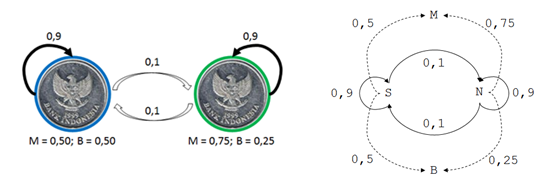
Untuk contoh ini, asumsikan saja bahwa kita
mengetahui probabilitas penukaran koin dan probabilitas masing-masing koin
untuk memberikan bagian muka dan belakang seperti pada Gambar 1 (panel kiri).
Nah sekarang pertanyaannya, jika kita mendapatkan urutan hasil pelemparan koin
berupa, katakanlah MMMBB, maka koin manakah yang paling mungkin untuk
memberikan hasil demikian untuk setiap hasil pelemparannya? Untuk menjawab
pertanyaan tersebut, mari kita gambarkan kembali probabilitas dari penukaran
antar koin (yang selanjutnya disebut probabilitas transisi) dan hasil yang
diberikan oleh masing-masing koin (yang selanjutnya disebut probabilitas emisi)
sebagai sebuah diagram HMM (Gambar 1, panel kanan). Dalam kasus ini, koin S dan
N merupakan bagian ‘hidden’ dari pemodelan HMM karena kita sebenarnya tidak
mengetahui dan hanya bisa membuat dugaannya untuk dimasukkan ke dalam pemodelan
HMM.
Jadi…..sebenarnya HMM itu apa sih? Well HMM dapat
didefinisikan sebagai sebuah pemodelan statistik terhadap fenomena Markov
process yang mengandung status (states) yang tidak terobservasi. Markov process
sendiri adalah sebuah model statistik yang mengasumsikan bahwa kondisi di masa
depan bergantung dari kondisi di masa sekarang. Dalam kasus pelemparan koin,
hasil yang diberikan dari setiap pelemparan koin merupakan Markov process. Nah
bagian 'hidden' nya adalah, kita tidak mengetahui ada koin lain yang digunakan
di dalam pelemparan tersebut yang dapat mempengaruhi hasil pelemparan. Jadi, di
dalam pemodelan HMM ini, kita akan memprediksi koin mana yang paling mungkin
digunakan oleh si bandar pada setiap pelemparan. Secara formal, HMM dicirikan
oleh empat komponen:
1.
Simbol (E, sigma) yang merupakan
hasil keluaran yang didapatkan dari penggunaan hidden states tertentu. Dua
simbol dalam kasus pelemparan koin adalah bagian muka (M) dan belakang (B).
2.
States
yang merupakan kumpulan dari hidden states. Dalam kasus pelemparan koin, hidden
states-nya adalah koin standar (S) dan non-standar (N).
3.
Matriks
probabilitas transisi yang berisi nilai probabilitas pertukaran antar states.
Dalam kasus pelemparan koin, matriks ini adalah matriks 2x2 antara N dengan S.
4.
Matriks
probabilitas emisi yang berisi nilai probabilitas munculnya hasil dari
pelemparan masing-masing states. Dalam kasus pelemparan koin, matriks ini juga
matriks 2x2 antara probabilitas M dan B masing-masing terhadap koin N dan S.
Untuk lebih
jelasnya, silahkan lihat Gambar 2.
 |
| Gambar 2. Empat komponen HMM. |
Setelah kita mengetahui komponen HMM,
selanjutnya kita perlu mengenal rumus utama di dalam pemodelan HMM yang
dituliskan dalam persamaan (1) berikut:
 |
| Maaf, karena di blog ini saia tidak bisa menuliskan simbol pi, jadinya saia ganti saja menjadi simbol p yah. |
Dimana Pr(x,p)
merupakan probabilitas dari HMM menggunakan jalur hidden state p
DAN memberikan hasil x. Nilai
probabilitas tersebut merupakan produk dari perkalian probabilitas HMM
memberikan hasil x JIKA menggunakan
jalur hidden state p [Pr(x|p)] terhadap probabilitas p [Pr(p)]
itu sendiri. Nah, daripada bingung terlalu lama, sebaiknya kita langsung
terapkan saja pada contoh pelemparan koin. Kembali ke pertanyaan, berapakah
probabilitas dari digunakannya koin dengan urutan state SNNNS untuk memberikan
hasil MMMBB. Oke, kondisinya adalah kita sudah mendapatkan urutan hidden state p
SNNNS dan probabilitas transisi serta emisi yang tertulis di Gambar 2. Untuk menghitung
probabilitasnya, pertama kita memodelkan diagram HMM menjadi semacam ‘grafik Viterbi’
dengan state S/N yang tersebar pada setiap urutan hasil (Gambar 3).
Selanjutnya, kita memberikan nilai probabilitas transisi yang mengikuti alur
state p yang telah diberikan, yakni SNNNS. Masih ada satu hal yang kurang,
yakni probabilitas pemilihan koin pada awal (Start --> S/N) dan akhir (S/N --> End). Untuk pemilihan koin pada awalan,
kita asumsikan saja bahwa kedua koin memiliki probabilitas sama besar (0,5);
sedangkan untuk mengakhiri pelemparan kita berikan nilai probabilitas 1 dari
nodus S/N menuju nodus End.
 |
| Gambar 3. Semacam ‘grafik Viterbi’ dari diagram HMM yang memuat pemodelan state koin S/N yang memberikan hasil urutan MMMBB. |
Sekarang, kita akan menandai jalur yang
dilewati oleh p (SNNNS) dan
memberikan nilai probabilitas menggunakan matriks transisi dan emisi. Diagram
HMM dengan jalur p yang sudah
ditandai dapat dilihat pada Gambar 4. Kita dapat melihat bahwa nilai
probabilitas yang disematkan pada tanda panah kecil di dalam semacam ‘grafik
Viterbi’ ini diambil dari matriks transisi; sedangkan nilai pada tanda panah
besar diambil dari matriks emisi. Dengan seluruh nilai probabilitas transisi
dan emisi ini kita dapat menghitung probabilitas kemunculan urutan MMMBB dari
penggunaan koin SNNNS sebagai produk perkalian keduanya. Well, nilai yang kita
dapatkan adalah 0,0001424 yang artinya probabilitas si bandar menggunakan koin
dengan urutan SNNNS untuk memberikan hasil MMMBB adalah sebesar 0,0001424.
Cukup kecil bukan??
 |
| Gambar 4. Diagram HMM dengan alur state p SNNNS yang memberikan hasil MMMBB. |
Mungkin ada teman yang bertanya, apakah ada
alur urutan penggunaan koin yang dapat memberikan pola probabilitas yang lebih
besar dari 0,0001424? Jawabannya dapat kita telusuri dari semacam ‘grafik
Vterbi’. Gambar 5 menampilkan seluruh nilai probabilitas transisi dan emisi
pada semacam ‘grafik Viterbi’ dan kita dapat menggunakannya untuk membandingkan
nilai probabilitas antar jalur p untuk mencari nilai tertinggi. Untungnya,
sifat dari HMM ini salah satunya adalah Markov property, yakni nilai
probabilitas suatu state di masa kini ditentukan dari satu state sebelumnya. Dengan
demikian, solusi dari permasalahan ini dapat diselesaikan dengan teknik pemrograman
dinamis (dynamic programming) seperti halnya pada melakukan penjajaran antar
dua urutan.
Misalnya, dari nodus Start ke state S/N
pertama; masing-masing nodus S dan N hanya memiliki satu arah dari nodus Start
sehingga nilai probabilitas untuk S1 adalah 0,5 x 0,5 = 0,25 dan untuk N1
adalah 0,5 x 0,75 = 0,375. Selanjutnya, untuk nodus S dan N kedua, kita perlu
mempertimbangkan dua skenario untuk masing-masing nodus:
S2 = S1 x 0,9 x 0,5 = 0,25 x 0,9 x 0,5 =
0,1125 (skenario 1)
= N1 x 0,1 x 0,5 = 0,375 x 0,1 x
0,5 = 0,01875 (skenario 2)
N2 = S1 x 0,1 x 0,75 = 0,25 x 0,1 x 0,75
= 0,01875 (skenario 1)
= N1 x 0,9 x 0,75 = 0,375 x 0,9
x 0,75 = 0,2531 (skenario 2)
Berlanjut
pada nodus S3 dan N3, kali ini kita perlu membandingkan empat skenario dari
masing-masing nodus. Kenapa empat? Karena nilai probabilitas pada S3 (atau N3)
diperoleh dari perbandingan nilai probabilitas S2 (atau N2) yang memiliki dua dua
skenario, sehingga:
S3 = S2 (dari skenario 1) x 0,9 x 0,5 = 0,1125
x 0,9 x 0,5 = 0,051 (skenario 1)
= S2 (dari skenario 2) x 0,9 x
0,5 = 0,01875 x 0,9 x 0,5 = 0,00844 (skenario 2)
= N2 (dari skenario 1) x 0,1 x
0,5 = 0,01875 x 0,1 x 0,5 = 0,0000938 (skenario 1)
= N2 (dari skenario 2) x 0,1 x
0,5 = 0,2531 x 0,1 x 0,5 = 0,013 (skenario 2)
 |
| Gambar 5. Semacam ‘grafik Viterbi’ dengan seluruh nilai probabilitas transisi dan emisi untuk lima pelemparan koin. |
Dan begitu
seterusnya untuk nodus keempat dan kelima. Hayo, sudah dihitung semua? Kalau begitu
sekarang saia tanya, urutan penggunaan koin mana yang paling mungkin memberikan
hasil pelemparan MMMBB? Yup, jawabannya adalah SSSSS dengan nilai probabilitas
sekitar 0,0102. Jika dibandingkan, penggunaan koin dengan urutan SSSSS memiliki
probabilitas 72 kali lebih besar daripada urutan SNNNS. Dengan demikian, kita
dapat menyimpulkan bahwa untuk lima lemparan koin pertama, si bandar masih
berlaku adil. Bagaimana jika untuk 10 lemparan berikutnya dengan keluaran hasil
BMMMBMMBBM? Silahkan dihitung sendiri yak..hehehe
Setelah cukup lelah membuat pemodelan HMM untuk
kasus pelemparan koin dan menghitung probabilitasnya, muncul pertanyaan
terakhir yang sekaligus menjadi penutup dari tulisan part 1 ini: Apa
hubungannya pemodelan koin ini dengan bioinformatika? Nanti pada tulisan part 2
saia akan membahas tentang pemodelan HMM seperti di atas yang diterapkan pada
penjajaran urutan protein. Tentunya model HMM yang digunakan akan lebih
kompleks dibandingkan yang sekarang digunakan dalam pelemparan koin, namun
konsepnya serupa. Ditunggu yak.
KohVic
1 komentar:
halo gan , numpang tanya sy bingung ngitung nodus keempat dan kelima
bisa kasi liat ga mas hasil nodus keempat dan kelima?
itu skenariony tetap 1 dan 2 aja?
tq
Posting Komentar